Approach
- Interfacial effects can be separated into individual contributions such as strain and internal electric field with computational experiments using density functional theory. Our group focuses on identifying the dominant contribution to emergent properties, which enables us to drive interesting materials properties via external stimuli such as biaxial strain, hydrostatic pressure, and electric/magnetic field.
- Our group has developed Python software libraries for enumerating orderings of multication sublattices. These atomically ordered compounds can be understood as a form of superlattice with varying periodicity of ordering and exhibit unexpected materials properties while the chemical stoichiometry is untouched.
Selected Publications
Tunable band structures in digital oxides with layered crystal habits
We use density functional calculations to show that heterovalent cation-order sequences enable control over band-gap variations up to several eV and band-gap closure in the bulk band insulator LaSrAlO4. The band-gap control originates from the internal electric fields induced by the digital chemical order, which induces picoscale band bending; the electric-field magnitude is mainly governed by the inequivalent charged monoxide layers afforded by the layered crystal habit. Charge transfer and ionic relaxations across these layers play secondary roles. This understanding is used to construct and validate a descriptor that captures the layer-charge variation and to predict changes in the electronic gap in layered oxides exhibiting antisite defects and in other chemistries.
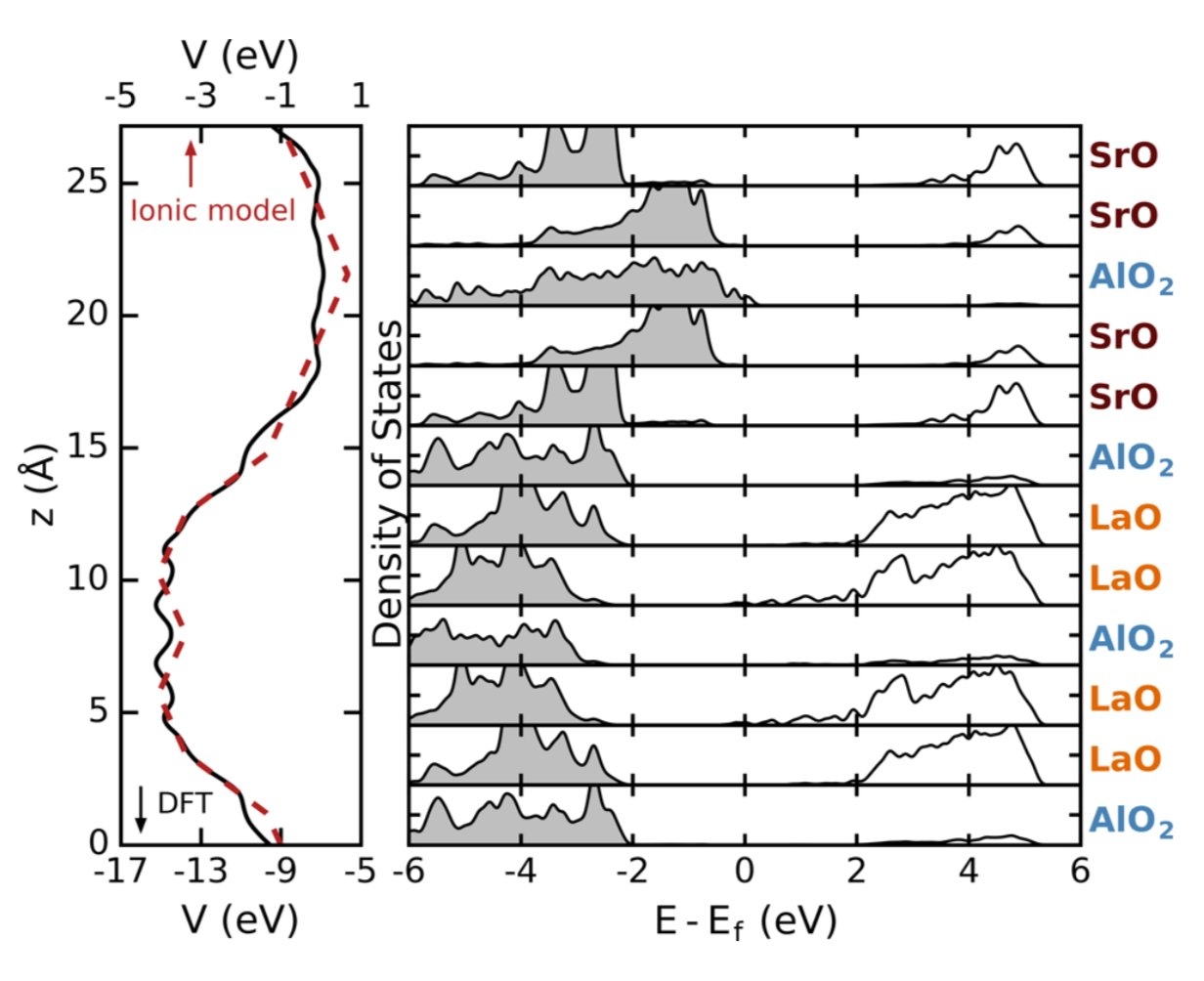
Figure: Averaged electrostatic potential energy (left) from DFT (black, bottom scale) and from the ionic model (red, top scale). Bilayer projected DOS for metallic LaSrAlO4 in variant 1.
Polar Oxides without Inversion Symmetry through Vacancy and Chemical Order
One synthetic modality for materials discovery proceeds by forming mixtures of two or more compounds. In transition metal oxides (TMOs), chemical substitution often obeys Vegard’s principle, and the resulting structure and properties of the derived phase follow from its components. A change in the assembly of the components into a digital nanostructure, however, can stabilize new polymorphs and properties not observed in the constituents. Here we formulate and demonstrate a crystal-chemistry design approach for realizing digital TMOs without inversion symmetry by combining two centrosymmetric compounds, utilizing periodic anion-vacancy order to generate multiple polyhedra that together with cation order produce a polar structure. We next apply this strategy to two brownmillerite-structured TMOs known to display centrosymmetric crystal structures in their bulk, Ca2Fe2O5 and Sr2Fe2O5. We then realize epitaxial (SrFeO2.5)1/(CaFeO2.5)1 thin film superlattices possessing both anion-vacancy order and Sr and Ca chemical order at the subnanometer scale, confirmed through synchrotron-based diffraction and aberration corrected electron microscopy. Through a detailed symmetry analysis and density functional theory calculations, we show that A-site cation ordering lifts inversion symmetry in the superlattice and produces a polar compound. Our results demonstrate how control of anion and cation order at the nanoscale can be utilized to produce acentric structures markedly different than their constituents and open a path toward novel structure-based property design.
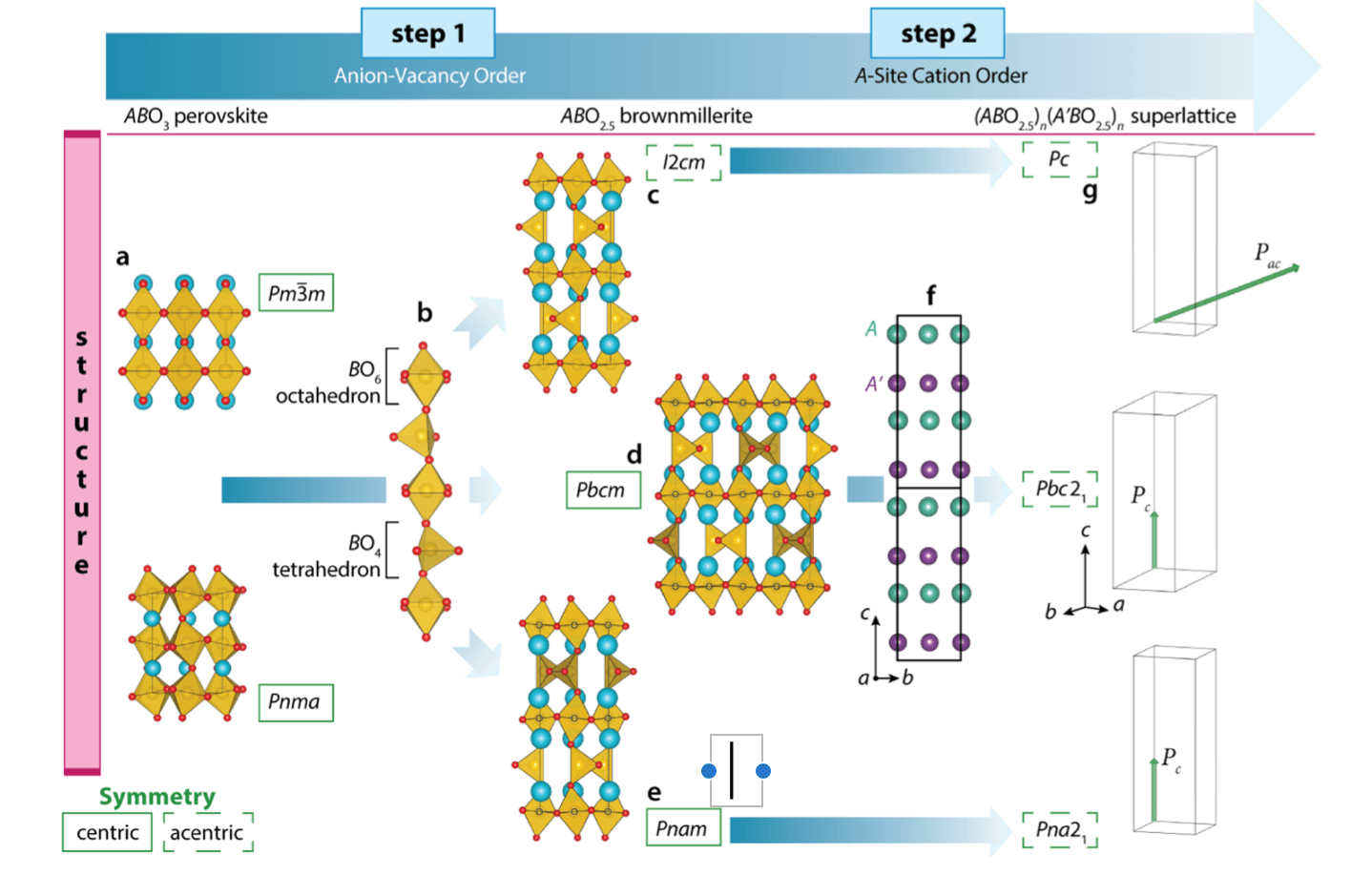
Figure: Design principles for realizing polar structures from nonpolar compounds through anion-vacancy and cation order. Starting from (a) fully oxidized perovskites are reduced in Step 1, resulting in (b) ordered rows of oxygen vacancies forming alternating layers of BO6 octahedra and BO4 tetrahedra. (c−e) Depict the resulting ABO2.5 brownmillerites: the polar I2cm and the nonpolar Pbcm and Pnam polymorphs that arise owing to the relative alignment of the BO4 tetrahedra. Inversion centers are located at sites with octahedrally coordinated B cations, indicated by black open circles; not shown are the inversion centers located on the unoccupied sites in the Pbcm and Pnam polymorphs. (f) In Step 2, chemically distinct A and A′ cations are ordered in layers along the ···BO6−BO4−BO6··· chain direction, which then removes all inversion centers and permits the net electric polarizations P indicated in (g).
Epitaxial-strain-induced polar-to-nonpolar transitions in layered oxides
Epitaxial strain can induce collective phenomena and new functionalities in complex oxide thin films. Strong coupling between strain and polar lattice modes can stabilize new ferroelectric phases from nonpolar dielectrics or enhance electric polarizations and Curie temperatures1 . Recently, strain has also been exploited to induce novel metal–insulator tran- sitions2,3 and magnetic reconstructions4–7 through its coupling to nonpolar modes, including rotations of BO6 transition-metal octahedra8. Although large strains are thought to induce ferroelectricity, here we demonstrate a polar-to-nonpolar transition in (001) films of layered A3B2O7 hybrid-improper ferroelectrics with experimentally accessible biaxial strains. We show the origin of the transition originates from the interplay of trilinear-related lattice mode interactions active in the layered oxides, and those interactions are directly strain tunable. Our results call for a careful re-examination of the role of strain–polarization coupling in ferroelectric films with nontrivial anharmonicities and offer a route to search for new functionalities in layered oxides.
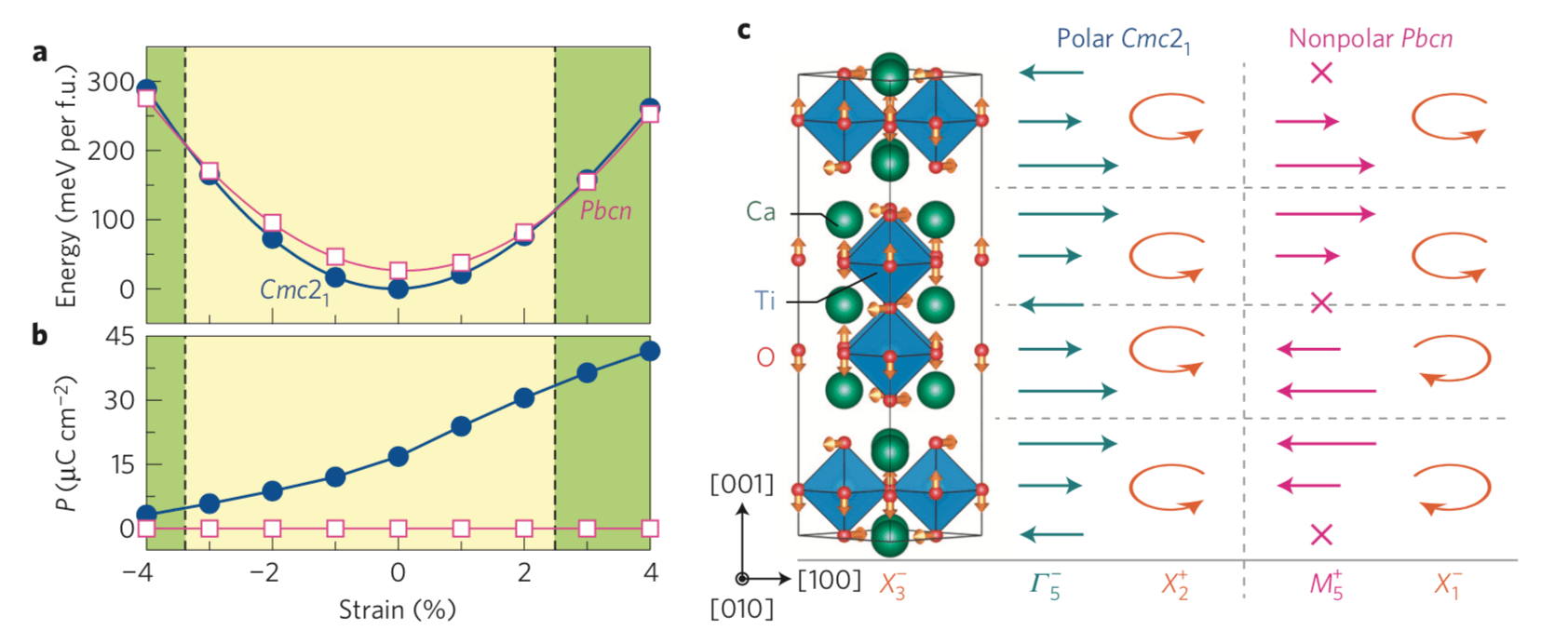
Figure: Strain dependence of the structure stability and electric polarization for (001) Ca3Ti2O7 films. (a) Calculated total energies as a function of biaxial strain, where the energy is given relative to that of the Cmc21 phase at 0% strain. For example at 3% and 4% strains, the nonpolar polymorph is more stable than the polar structure by approximately 3.1 and 8.3 meV per formula unit (f.u.), respectively. The dashed vertical lines indicate the critical strain values for the P–NP transition and separate strain ranges over which the polar (yellow shaded) and nonpolar (green shaded) structures are stable. (b) Electric polarization versus strain for the polar Cmc21 and nonpolar Pbcn phases. (c) Illustration of the distortion modes in the Cmc21 and Pbcn phases with respect to the high-symmetry I4/mmm reference structure. The structure (left) shows the RP crystal with two-dimensional layers of corner-connected TiO6 polyhedra. The arrows on the oxide ions indicate the displacement pattern for the out-of-phase OOT about [ ̄110], which transforms as irrep X3−. The displacement modes described by Γ5− and M5+ induce layer polarizations with the direction and magnitude indicated schematically by the teal or pink arrows. Orange arrowed arcs indicate the BO6 rotation sense in each perovskite layer. In contrast to the HIF Cmc21 phase, the combination of the QX1– and QX3– modes in Pbcn, respectively, describing the OOR and OOT, does not lift inversion symmetry. Note that the Γ5− mode produces a macroscopic electric polarization, whereas the M5+ mode does not induce a macroscopic electric polarization; the cross in M5+ indicates there is no layer dipole. The coordinate system is set to a pseudotetragonal system of the perovskite unit cell.