Approach
- Ab initio calculations and analyses. This study is mainly based on the density functional theory calculations implemented in various tools, e.g., Vienna Ab Initio Simulation Package and Quantum Espresso software suite. Phonon calculations and Wannier-90 calculations are also performed to determine the dynamical stability and analyze the electronic band structure of the crystal structures, respectively.
- Genetic algorithm structure search. A lower energy structure search method to help establish the phase diagram under strain at 0K.
- Landau model. On the basis of the space group of the crystal structure, we can build a phenomenological model (i.e., Landau model) to elucidate the microscopic mechanism on the phase transitions. In this model, the atomic displacements can be described by several types of collective displacements in terms of modes, such as polar mode and oxygen octahedral mode, which consists of the basis set in the Landau model.
- Monte Carlo simulations. The parallel tempering Monte Carlo (PTMC) simulations to simulate the magnetic transition temperature (i.e., TN for antiferromagnetic material and TC for ferromagnetic material), based on the a spin Hamiltonian comprised of the Heisenberg symmetric exchange interaction, antisymmetric Dzyaloshinskii-Moriya (DM) interaction, and single-ion anisotropy (SIA).
- Tight-binding model. A method based on the Bloch theory to treat the electronic state for a system and build the electronic band structure, which captures the important orbital interactions contributing to the electronic state in the band structure.
Selected Publications
Room Temperature Electric-Field Control of Magnetism in Layered Oxides with Cation Order
Searching for materials with room-temperature electric-field control of magnetism has interested researchers for many years with three-dimensional perovskite BiFeO3-based compounds as the main focus. Here we choose the layered hybrid improper ferroelectric Ruddlesden-Popper oxides as a plat- form from which to realize electric field controllable magnetism, leveraging a recently identified strain tunable polar-to-nonpolar (P-NP) transition. We first propose a design principle for selecting the required A and B cation chemis- tries that will ensure (001) A3B2O7 films exhibit P-NP transitions, which we substantiate with density functional calculations. By extending the guideline to B-site ordered A3BB′O7 oxides, we identify more compounds exhibiting P-NP transitions marked by the disappearance of an in-plane polarization that can be functionalized. We then demonstrate that weak ferromagnetism can be tuned by an electric field at the boundary of the P-NP transition in B-site ordered (001) A3BB′O7 magnetic films, based on which we predict that cation ordered Ca3TcTiO7 may be a viable candidate for room-temperature electric-field control of magnetism.
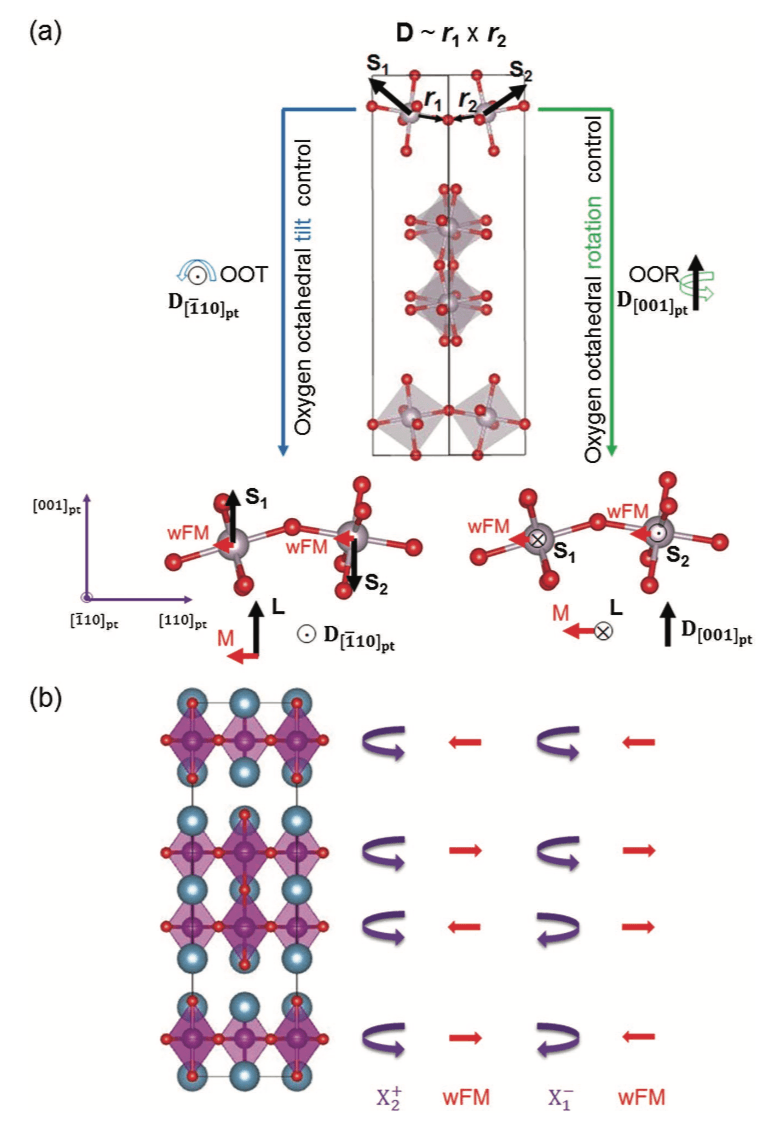
Figure: Mechanisms available for oxygen octahedral controllable magnetism. (a) shows the mechanisms for oxygen octahedral tilt (left, blue) and rotation (right, green) control. Si (i = 1,2), Di (i = 1,2), ri (i = 1,2), M and L represent the local spin vectors, DM-interaction vectors, unit vectors along the Si-O bond direction, and the wFM and AFM vectors, respectively. The polar Cmc21 structure (center) is shown as reference without the A cations for clarity along with the pseudotetragonal axes. b) Illustration of how the wFM vector changes upon reversing the sense of the OOR in the perovskite block of the A3B2O7 Ruddlesden–Popper I4/mmm structure. Purple arrowed arcs indicate the BO6 rotation sense in each perovskite layer. Red arrows indicate the direction of the wFM. Note that the net magnetization is always zero in both cases.
Tunable inversion symmetry to control indirect-to-direct band gaps transitions
Electric-field tunable indirect-to-direct band gap transitions occur in thin-film silicon and transition metal dichalcogenides; however, they remain challenging to access in three-dimensional transition metal oxides. Very recently, an unusual polar-to-nonpolar phase transition under epitaxial strain was discovered in A3B2O7 hybrid improper ferroelectrics (HIFs), which supports controllable dielectric anisotropy and magnetization. Here we examine HIF (ABO3)1/(A BO3)1 superlattices and AA BB O6 double perovskites and predict a competing nonpolar antiferroelectric phase, demonstrating it is hidden in hybrid improper ferroelectrics exhibiting corner-connected BO6 octahedra. Furthermore, we show the transition between the polar and nonpolar phases enables an in-plane electric field to control the indirect-to-direct band gap transition at the phase boundary in the (ABO3)1/(ABO3)1 superlattices and AA BB O6 double perovskites, which may be tuned through static strain or chemical substitution. Our findings establish HIFs as a functional electronics class from which to realize direct gap materials and enables the integration of a broader palette of chemistries and compounds for linear and nonlinear optical applications.
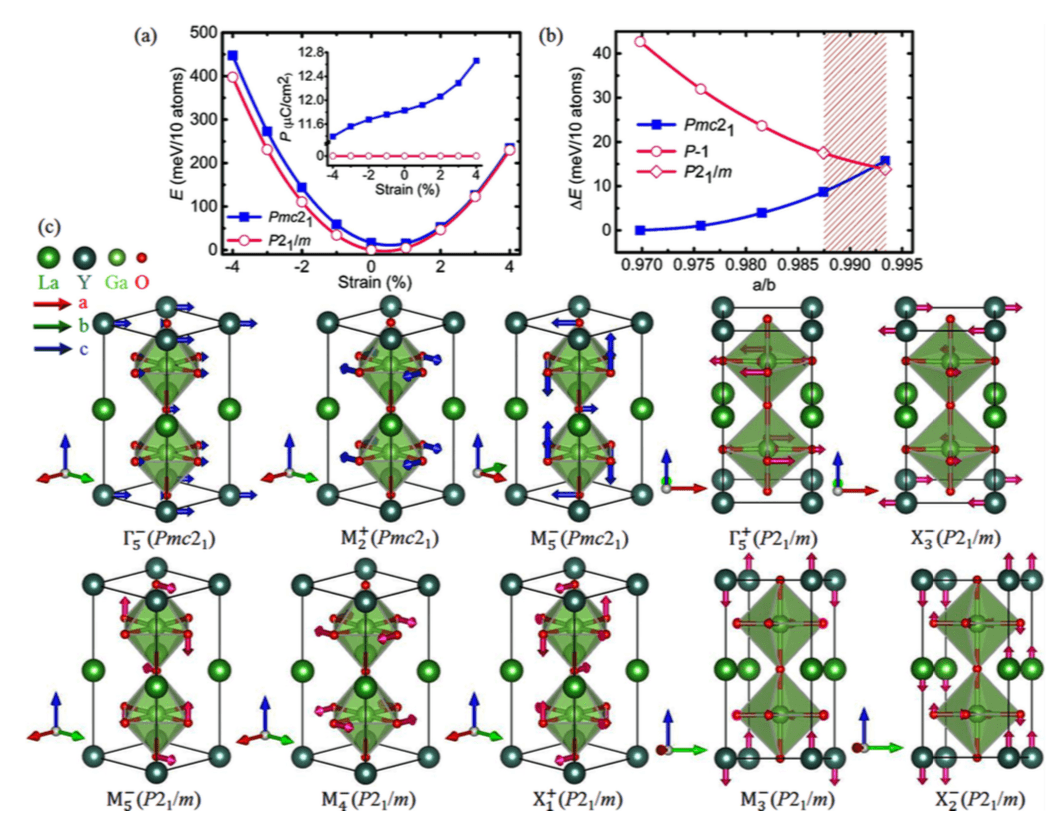
Figure: (a) Calculated total energies as a function of biaxial strain, where the energy is given relative to that of the P21/m phase at 0% strain in LaGaO3/YGaO3. Inset: polarization versus strain in the two phases where the polarization in Pmc21 phase is along [11 ̄0] direction. (b) Calculated total energies versus the in-plane a/b lattice parameter ratio in LaGaO3/YGaO3, where the energy is given relative to that of the Pmc21 phase in bulk. The P21/m structure exhibits P1 ̄ symmetry (open circle) when the in-plane lattice parameters are constrained to be those of Pmc21 at each a/b value whereas this P1 ̄ structure transforms back to P21/m (open diamond) after structural relaxation with a/b ∼ 1 as indicated by the hatched area. (c) Active symmetry-adapted modes in P mc21 and P 21/m, which are obtained by decomposing the ion displacements in each structure with respect to P4/mmm. Only ion displacements in the 10-atom formula unit are shown for clarity, with the arrows indicating the direction and magnitude of the ion displacements.