Probing Ultrafast/Metastable Phases

Nonlinear optical manipulation is a promising route to switch a material between different phases at the femtosecond timescale. It has been used to induce transient superconductivity in both cuprates and fullerene-based compounds, to remove the charge ordering in manganites, and to excite the silent mode in traditional dielectrics. With this approach we can dynamically access novel states which are forbidden or hard to reach in equilibrium.

Approach

Based on structure-properties relationship, we theoretically study the competing states of nonequilibrium structures. These transient structures can be accessed by intensive excitation of coupled phonon normal modes, or optical excitation of electrons to high energy orbitals. By mapping out the energy profile between different states we can understand the experimentally observed metastable phases and try to predict the path of phase evolution during the dynamical process.

Selected Publications

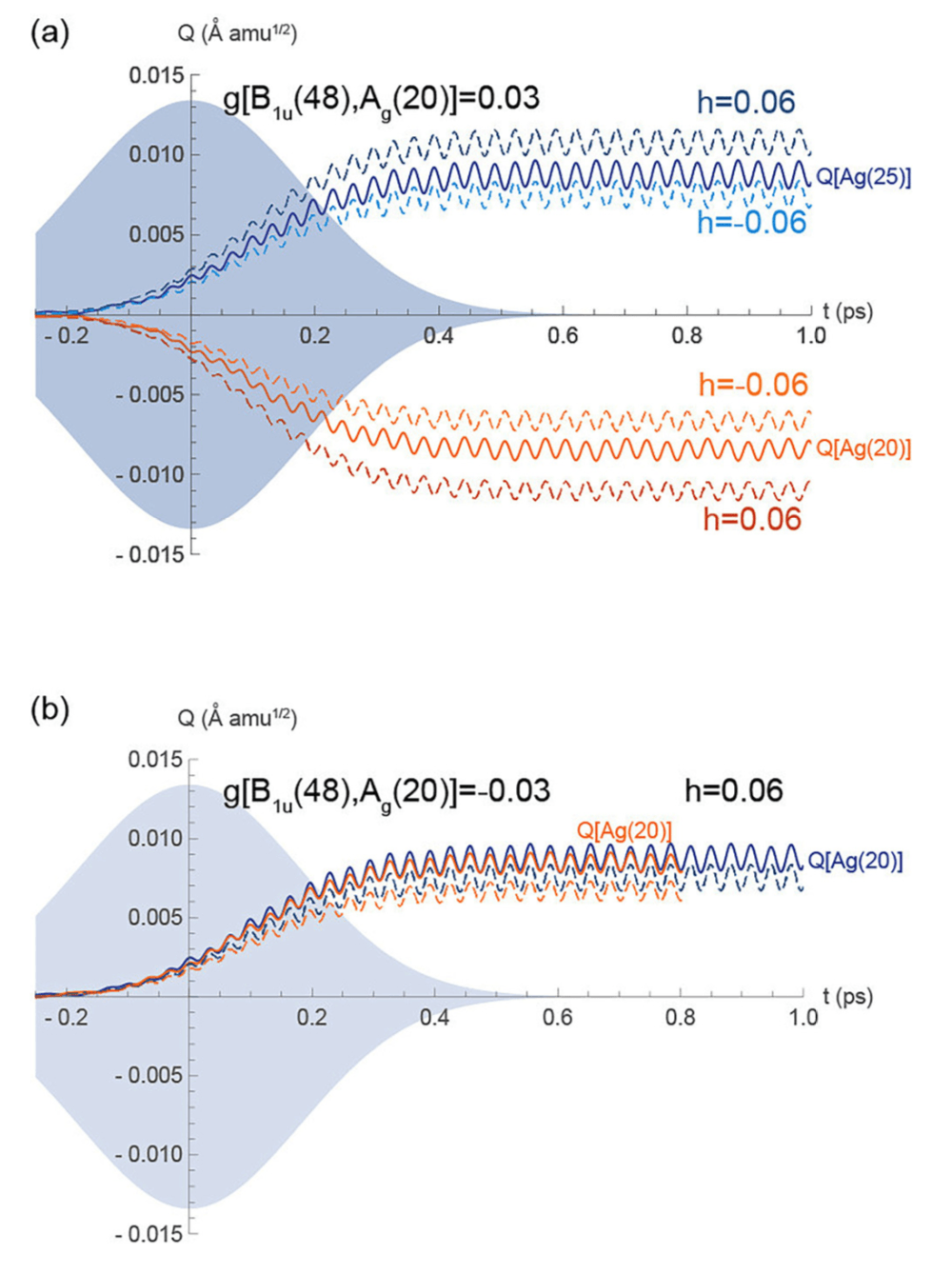
Coupled Raman-Raman modes in the ionic Raman scattering process

We employ a lattice Hamiltonian to examine the dynamics of coupled normal modes excited through a nonlinear phononic process, extending the model beyond infrared and first-order Raman active mode couplings to include interactions between symmetry-allowed Raman active modes. We examine the strength of the interactions between two Raman active modes on the targeted driven-mode dynamics to confirm that all symmetry allowed Raman modes interact with each other. We apply the model to the correlated insulating ferromagnet YTiO3 and present the resulting renormalization effects on the driven-mode dynamics from the anharmonic interactions. Owing to the dependence of the displacive amplitude of the Raman active mode on such interactions, espe- cially for those modes with small amplitude, we suggest that models of anharmonic phononic cou- pling in materials with electronic, ferroic, or superconducting properties derived from competing Raman-like distortions should include these low-order terms in the equations of motion describing the excited phonons to obtain accurate physical models. Published by AIP Publishing.

Figure: Dynamics of the two coupled Raman modes at small h. The effects of reversing the sign of h and g are shown in (a) and (b), respectively.

Ultrafast Band Engineering and Transient Spin Currents in Antiferromagnetic Oxides

We report a dynamic structure and band engineering strategy with experimental protocols to induce indirect-to-direct band gap transitions and coherently oscillating pure spin-currents in three- dimensional antiferromagnets (AFM) using selective phononic excitations. In the Mott insulator LaTiO3, we show that a photo-induced nonequilibrium phonon mode amplitude destroys the spin and orbitally degenerate ground state, reduces the band gap by 160 meV and renormalizes the carrier masses. The time scale of this process is a few hundreds of femtoseconds. Then in the hole-doped correlated metallic titanate, we show how pure spin-currents can be achieved to yield spin-polarizations exceeding those observed in classic semiconductors. Last, we demonstrate the generality of the approach by applying it to the non-orbitally degenerate AFM CaMnO3. These results advance our understanding of electron- lattice interactions in structures out-of-equilibrium and establish a rational framework for designing dynamic phases that may be exploited in ultrafast optoelectronic and optospintronic devices.

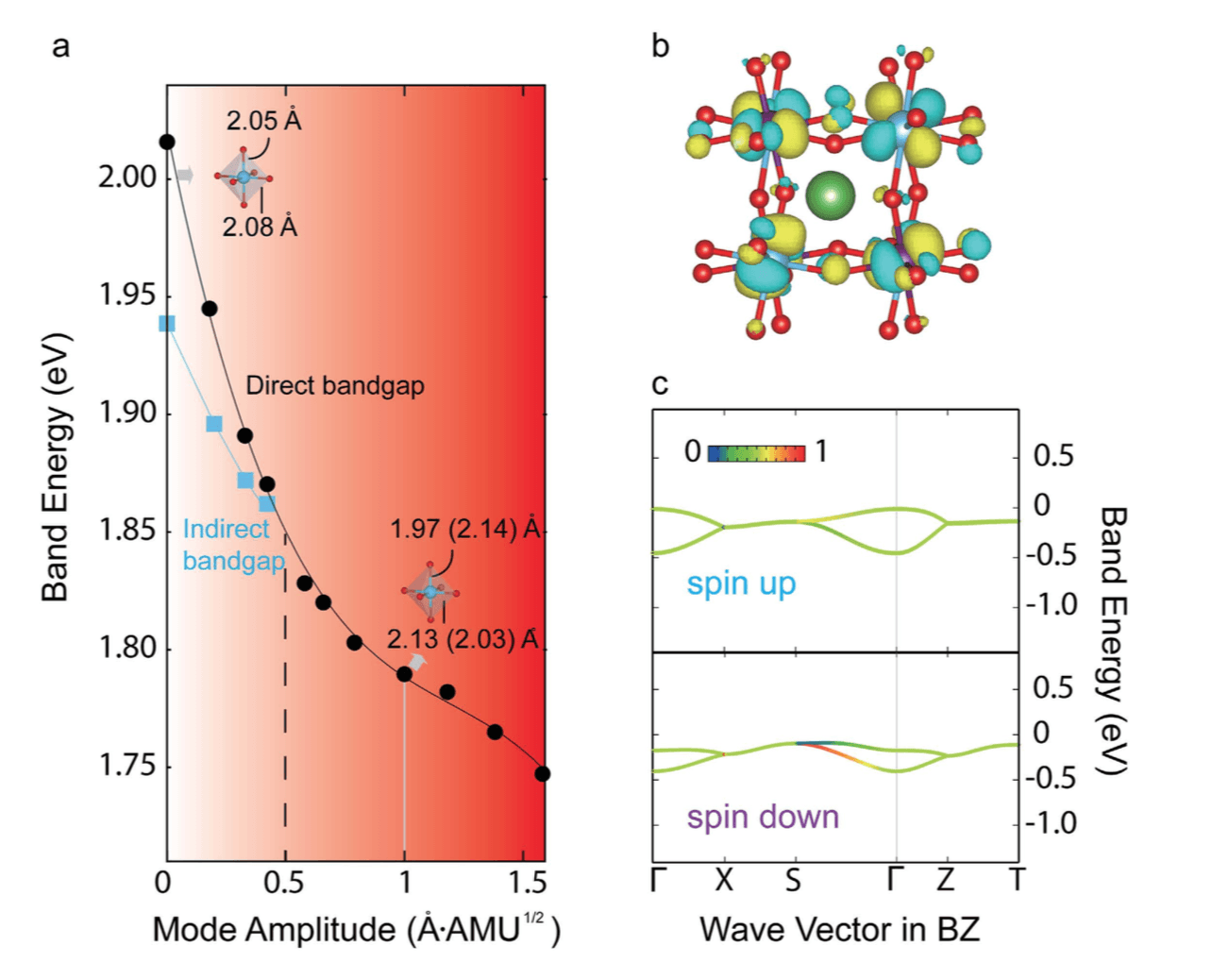
Figure: Origin of the indirect-to-direct band gap transition with nonequilibrium FOJT bond distortions.

(a) The band evolution as a function of the Q3 normal mode amplitude. The broken vertical line shows the transition point at the critical Qc ~ 0.5 Å AMU1/2. The insets in (a) indicate the change in Ti-O bond distances at different values of the mode amplitude. (b) The MLWFs for the lower Hubbard bands shows enhanced orbital ordering at Q = 1 Å AMU1/2. (c) The projected valence bands (color scale) on to the two t2g orbitals (dxz = 0 and dyz = 1). The spin up valence band edge is at the Γ point.