Approach
- We perform density functional theory (DFT) simulations to study the crystal and electronic structures of transition metal compounds in different electronic states. Properties of interest typically include lattice constants, electronic structures (band structures, density of states, dielectric constants), lattice dynamics (phonon dispersions), and thermodynamic properties. We utilize the link between these features and the macroscopic response to understand and design new materials exhibiting novel transitions between various phases.
Selected Publications
Electronic properties of bulk and thin film SrRuO3: Search for the metal-insulator transition
We calculate the properties of the 4d ferromagnet SrRuO3 in bulk and thin film form with the aim of understanding the experimentally observed metal-to-insulator transition at reduced thickness. Although the spatial extent of the 4d orbitals is quite large, many experimental results have suggested that electron-electron correlations play an important role in determining this material’s electronic structure. In order to investigate the importance of correlation, we use two approaches which go beyond the conventional local-density approximation to density-functional theory (DFT): the local spin-density approximation + Hubbard U (LSDA+U) and the pseudopotential self-interaction correction (pseudo-SIC) methods. We find that the details of the electronic structure predicted with the LSDA do not agree with the experimental spectroscopic data for bulk and thin film SrRuO3. Improvement is found by including electron-electron correlations, and we suggest that bulk orthorhombic SrRuO3 is a moderately correlated ferromagnet whose electronic structure is best described by a 0.6 eV on-site Hubbard term, or equivalently with corrections for the self-interaction error. We also perform ab initio transport calculations that confirm that SrRuO3 has a negative spin polarization at the Fermi level, due to the position of the minority Ru 4d band center. Even with static correlations included in our calculations we are unable to reproduce the experimentally observed metal-insulator transition, suggesting that the electronic behavior of SrRuO3 ultrathin films might be dominated by extrinsic factors, such as surface disorder and defects, or due to dynamic spin correlations which are not included in our theoretical methods.
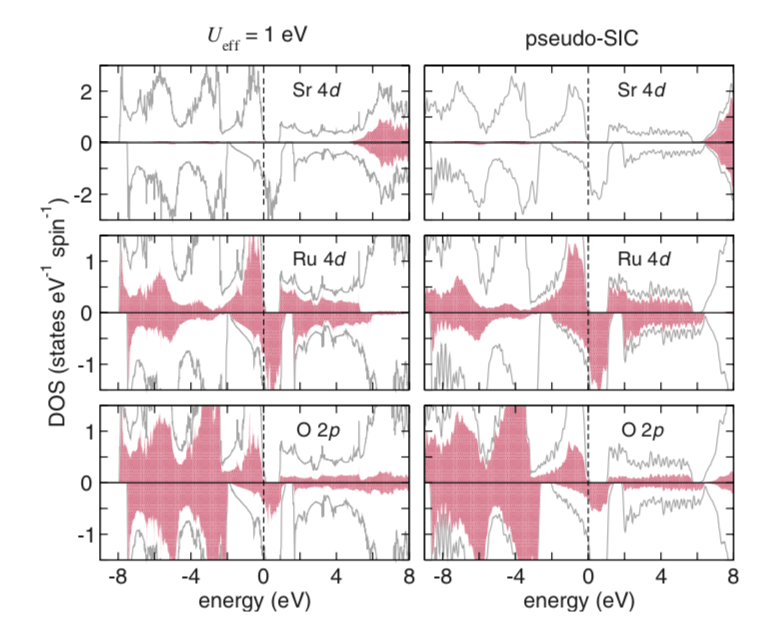
Figure: (Color online) The total (gray line) and partial spin-resolved (shaded) density of states for orthorhombic SrRuO3 calculated with Ueff = 1eV (left) and pseudo-SIC (right) are shown in each panel. (Upper) Sr 4d states, (middle) Ru 4d states, and (lower) O 2p states.
Tunable metal-insulator transition, Rashba effect and Weyl Fermions in a relativistic charge-ordered ferroelectric oxide
Controllable metal–insulator transitions (MIT), Rashba–Dresselhaus (RD) spin splitting, and Weyl semimetals are promising schemes for realizing processing devices. Complex oxides are a desirable materials platform for such devices, as they host delicate and tunable charge, spin, orbital, and lattice degrees of freedoms. Here, using first-principles calculations and symmetry analysis, we identify an electric-field tunable MIT, RD effect, and Weyl semimetal in a known, charge-ordered, and polar relativistic oxide Ag2BiO3 at room temperature. Remarkably, a centrosymmetric BiO6 octahedral-breathing distortion induces a sizable spontaneous ferroelectric polarization through Bi3+/Bi5+ charge disproportionation, which stabilizes simultaneously the insulating phase. The continuous attenuation of the Bi3+/Bi5+ disproportionation obtained by applying an external electric field reduces the band gap and RD spin splitting and drives the phase transition from a ferroelectric RD insulator to a paraelectric Dirac semimetal, through a topological Weyl semimetal intermediate state. These findings suggest that Ag2BiO3 is a promising material for spin-orbitonic applications.
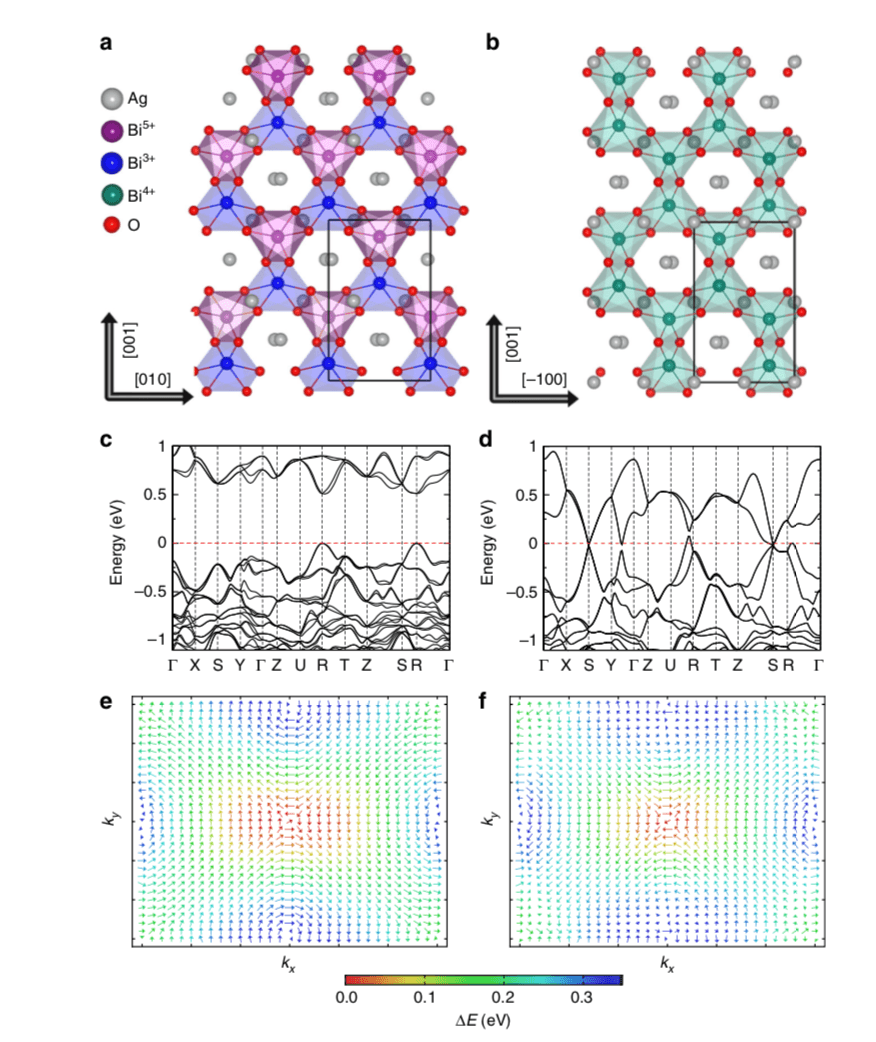
Figure: Structural and electronic properties of Ag2BiO3. Crystal structure of (a) the ferroelectric Pnn2 and (b) the hypothetical paraelectric Pnna phase. Red, gray, green, blue, and purple spheres are O2−, Ag+, Bi4+, Bi3+, and Bi5+ ions, respectively. (c) and (d) are the band structures of the Pnn2 and Pnna phases, respectively. The Fermi level is shifted to 0 eV. High symmetry points in the first Brillouin zone are defined in Supplementary Figure 1. € and (f) are the spin textures of the inner and outer branches of conduction bands at the R point in the polar Pnn2 phase. The color code indicates the energy level with respect to the bottom of conduction band.